本記事は、2010年ごろに「はてなダイアリー」で執筆したものを一部修正したものです。

Problem 18 「最大経路の和 その1」

まずはこちらをご覧ください。

こちらは「算数・数学の問題をプログラミングで解こう！」でおなじみ、Project Euler の問題です。日本語に翻訳されているサイト¹があり、今回はこちらのサイトから引用させていただきました。

というわけで、さっそくこの問題²を解いてみます。

#
# e18.rb - Project Euler Problem 18 「最大経路の和 その1」を解く
#
# https://projecteuler.net/problem=18
#

data = File.read(ARGV[0]).split("\n").map{|e| e.split(" ").map{|ee| ee.to_i }}
# [[3], [7, 4], [2, 4, 6], [8, 5, 9, 3]]

num = data.length - 1
sum = lambda{|arr| arr.inject(:+) }

all = (0..2**num-1).map{|i|
  route = (0..num-1).map{|idx| i[idx] }.reverse
  xidxs = [0] + (0..num-1).map{|idx| sum[route[0..idx]] }
  vals  = xidxs.each_with_index.map{|x,y| data[y][x] }
  sum[vals]
}

p all.max # 各経路の和の最大値

方針はシンプルで、全ての経路の和を導出してその最大値を求める、というものです。

経路の選択は 1 段目から順に「左か右か」なので、これを 0/1 で表現することを考えると、経路は段数 n を使って 2^(n-1) 通り存在し、0～(2^(n-1)-1) までの数字を二進数に変換するとそれぞれ別々の経路と対応する、ということになります。

今回の実装の場合、「k段目までに右を選択した回数＝k段目の配列のインデックス」になりますので、これを用いて実際の経路で通った数字を配列にします。

たとえば、上の 4 段の三角形の場合は選択肢が 2^(4-1) = 8 通りなので、以下のような感じになります。

#    3
#   7 4
#  2 4 6
# 8 5 9 3
      route          xidxs             vals             sum[vals]
0 -> [ 0, 0, 0 ] -> [ 0, 0, 0, 0 ] -> [ 3, 7, 2, 8 ] -> 20
1 -> [ 0, 0, 1 ] -> [ 0, 0, 0, 1 ] -> [ 3, 7, 2, 5 ] -> 17
2 -> [ 0, 1, 0 ] -> [ 0, 0, 1, 1 ] -> [ 3, 7, 4, 5 ] -> 19
3 -> [ 0, 1, 1 ] -> [ 0, 0, 1, 2 ] -> [ 3, 7, 4, 9 ] -> 23
4 -> [ 1, 0, 0 ] -> [ 0, 1, 1, 1 ] -> [ 3, 4, 4, 5 ] -> 16
5 -> [ 1, 0, 1 ] -> [ 0, 1, 1, 2 ] -> [ 3, 4, 4, 9 ] -> 20
6 -> [ 1, 1, 0 ] -> [ 0, 1, 2, 2 ] -> [ 3, 4, 6, 9 ] -> 22
7 -> [ 1, 1, 1 ] -> [ 0, 1, 2, 3 ] -> [ 3, 4, 6, 3 ] -> 16

このプログラムを、下の 15 段の三角形に適用すると、以下のような結果になります。

$ cat triangle18-2.txt
75
95 64
17 47 82
18 35 87 10
20 04 82 47 65
19 01 23 75 03 34
88 02 77 73 07 63 67
99 65 04 28 06 16 70 92
41 41 26 56 83 40 80 70 33
41 48 72 33 47 32 37 16 94 29
53 71 44 65 25 43 91 52 97 51 14
70 11 33 28 77 73 17 78 39 68 17 57
91 71 52 38 17 14 91 43 58 50 27 29 48
63 66 04 68 89 53 67 30 73 16 69 87 40 31
04 62 98 27 23 09 70 98 73 93 38 53 60 04 23

$ time ruby e18.rb triangle18-2.txt
1074

real    0m0.386s
user    0m0.380s
sys     0m0.004s

実行時間は0.4秒ほど。楽勝ですね！

Problem 67 「最大経路の和 その2」

では、次の問題をご覧ください。³

15段で0.4秒だから、100段でも1分かからないくらいで終わるかな？

ちょっとお試ししてみよう。まず手始めに、15行から一つずつ増やしてみた。

16段 ⇒ 0.7秒
17段 ⇒ 1.5秒
18段 ⇒ 3.0秒
19段 ⇒ 6.0秒 # あれ？倍？
20段 ⇒ 13 秒 # さらに倍？
21段 ⇒ 31 秒 # あ、これ倍々になってあかんやつや…

何かおかしいなと思い、問題文をよく見てみると…

これは, Problem 18のずっと難しいバージョンです. 全部で 2^99 通りの組み合わせがあるので, この問題を解決するためにすべてのルートをためすことは可能でありません！ あなたが毎秒1兆本の (10^12) ルートをチェックすることができたとしても, 全てをチェックするために200億年以上かかるでしょう.

200億年！！宇宙の歴史！！(￣□￣;

2^99 という果てしない回数の計算をすることは不可能というわけで、別の方法を模索する必要がありそうです。

動的計画法

問題文には続きがあり、

解決するための効率的なアルゴリズムがあります. ;o)

ということです。ここでは、「動的計画法」⁴というアルゴリズムを使用することを考えます。

ポイント(1) 計算結果の保存

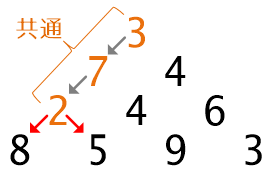
先ほどの解き方で、99段めまで同じ経路で100段目を選ぶときに左右に分かれたとすると、分かれるまでの途中計算はすべてまるっと繰り返されていることになる。これは無駄ですね。99段めまでの結果が保存されていれば、計算を繰り返さなくてもいいなぁ。。という着想ができます。

ポイント(2) 枝刈り

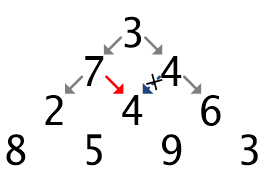
例で「 3 ⇒ 4 ⇒ 4 」と選択していく経路は、最大値を求めるという観点では「 3 ⇒ 7 ⇒ 4 」という経路よりも小さくなります。つまり、3 段目の真ん中を通る場合、2 段目での 4 という選択肢を無視することができるということですね。また、「 3 ⇒ 4 ⇒ 4 」の経路はこの先一切計算する必要はないということにもなります。

コーディングの方針

これらのポイント(1)「計算結果の保存」と(2)「枝刈り」とを組み合わせる手法を動的計画法といいます。

各経路の合計を記録しつつ、枝刈りする過程を図にすると、こんな感じ。

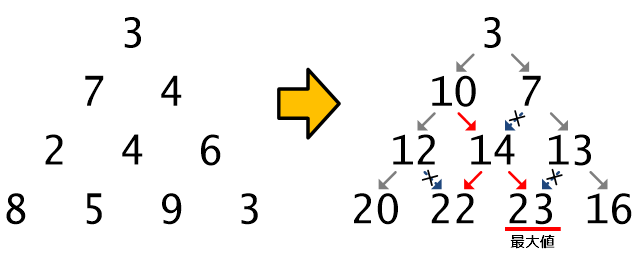
これを式で考えます。

\(i\) 段目で左から\(j\) 番目の値を\(a_{i,j}\) 、同じ位置までの経路の和の最大値を\(S_{i,j}\) とすると、\(S_{i,j}\) には以下の式が成り立ちます。今回は Ruby の配列の実装に合わせて \(i,j=0,1,2,...\) で、頂点を \(i=0, j=0\) と考えています。

• \(i=0\) のとき : \(S_{0,0} = a_{0,0}\)
• \(i\neq 0\) のとき :
  • \(j=0\) （左端）のとき : \(S_{i,0} = S_{i-1,0} + a_{i,0}\)
  • \(j=i\) （右端）のとき : \(S_{i,i} = S_{i-1,i} + a_{i,i}\)
  • \(j\neq 0,\ j\neq i\) のとき : \(S_{i,j} = \max( S_{i-1,j-1}, S_{i-1,j} ) + a_{i,j}\)

この式に従うと、0段目から順次\(S_{i,j}\) を求めていくことができます。すべての位置について計算後、最下段の値のうち最大のものが、求める値ということになります。

コーディング

検討結果に従ってコーディングをしてみました。

#
# e67.rb - Project Euler Problem 67 「最大経路の和 その2」を解く
#
# https://projecteuler.net/problem=67
#

a = File.read(ARGV[0]).split("\n").map{|e| e.split(" ").map{|ee| ee.to_i }}
s = a.clone

s.length.times{|i|
  next if i == 0
  s[i].length.times{|j|
    upper_left  = ( j == 0 ) ? nil : a[i-1][j-1] # 左端の場合、左上が存在しない
    upper_right = ( j == i ) ? nil : a[i-1][j]   # 右端の場合、右上が存在しない
    s[i][j] = a[i][j] + [ upper_left, upper_right ].compact.max
  }
}

p s[-1].max # 最終段の最大値

これを実行すると、

$ time ruby e67.rb triangle.txt
7273

real    0m0.076s
user    0m0.072s
sys     0m0.000s

正解いただきました！しかも一瞬です！

まとめ

Project Euler の Problem 18 および 67 を題材に、基本的な動的計画法の考え方について紹介しました。

いきなり n=100 を最初のプログラムに解かせようとしていたら、大変なことになっていましたね。アルゴリズムは大事。

総当たりだと 200 億年かかる計算も、0.08秒で。恐るべし、動的計画法。

おまけ

今回紹介したコードおよび入力データを github に登録しています。

yoshidaa/project-euler-solutions: Project Euler

参考

1. Project Euler - PukiWiki - odx ↩

2. Problem No.18(日本語) ↩

3. Problem No.67(日本語) ↩

4. 動的計画法 ↩