仕事・趣味を問わずプログラミングをする機会があるのですが、ふと、「プログラミングでダーツのシミュレーション的なことができないかな？」 と思い立ちました。ゼロワンで最適なアレンジを計算したり、クリケットの戦略検討ができたり、、、などなど、いろいろ参考になる情報が得られたらいいなあという夢がふくらみます。

手始めに過去の文献¹や記事²を調べてみたところ、

• ダーツの各スローにおける到達位置が、目標位置を中心とした正規分布に従う

というのが比較的手軽かつ一般的な方法ということがわかりました。そこで本記事では ダーツプログラミング を行っていくためにこの正規分布³が基本的な道具であると考え、正規分布をダーツプログラミングで扱うための基本的な事項について紹介していきます。

ダーツのスローと正規分布

正規分布は一言で言うと「同じ条件のもとで得られた、ばらつきのある事象の発生頻度を調べてみると、中央の値の発生頻度が最も多く、それを中心に対称形で発生頻度が少なくなるという現象のこと」です。

正規分布

たとえば学校のテストの偏差値なども「平均に近い人の割合が大きい」という、正規分布の考え方が用いられており、上記の図でいうところの 0 が偏差値 50 、$\sigma$ (上位15.8%ライン) が偏差値 60、$2\sigma$ (上位2.2%ライン)が偏差値 70 ということになります。

ダーツは平面に向かって投げる競技なので、分布は二次元的になります。次に示す図は、横方向と縦方向のばらつきが同じくらいだったとして、ブルの中心を狙って投げた場合の確率分布のイメージです。中心に近いほど到達する確率が高く、ブルからの距離が離れるほど到達する確率が低くなることがわかります。

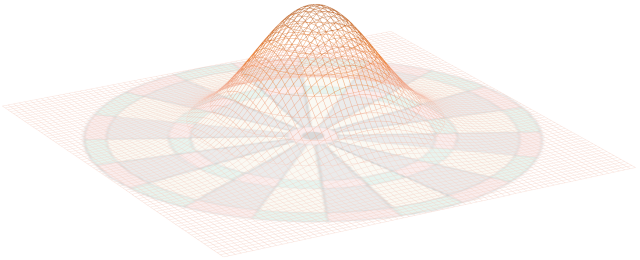
正規分布とダーツボード

ダーツをある目標に向かって投げたとき、その到達位置が 二次元正規分布 ⁴ に従うと仮定します。このとき、目標とする位置を$(\overline{x}, \overline{y})$、実際に到達する位置を$(x, y)$、横方向のばらつきを $\sigma_x$、縦方向のばらつきを $\sigma_y$、$x$方向と$y$方向のばらつきは独立であるとすると、$(x,y)$ に刺さる確率 $f(x,y)$ は以下のように表すことができます。

\[f(x,y) = \frac{1}{2\pi\sigma_x\sigma_y}\exp\Bigl(-\Bigl(\frac{(x-\overline{x})^2}{2\sigma_x^2}+\frac{(y-\overline{y})^2}{2\sigma_y^2}\Bigr)\Bigr) \;\;\; \cdots (1)\]

本記事では、ダーツのスローがこの正規分布の式に従うと仮定して進めたいと思います。

ここで注意しておきたいのは「正規分布よりも精密に近似できるモデルがある¹」「正規分布に従わないとする考え方もある⁵」、ということです。そもそもダーツは個人の投げ方やクセ、その日の体調やメンタルによる影響が多分にあるため、実際の分布が正規分布に従うとは限りません。

ただ、個人的には「分布の正確性や計算結果の精密さを追求するよりも、簡易的なモデルであってもそこから得られる知見や考え方にフォーカスする」ことで、得られるものも多いのではと考えていますので、現段階ではこの式(1)をベースにするモデルで十分なのではないかと思っています。

ブル率と標準偏差 $\sigma$

ダーツはプレーヤーのレベルによって、狙った位置に対する到達位置のばらつきが大きく変わります。このばらつきは、式(1)における標準偏差 $\sigma_x$ および $\sigma_y$ で表されるのですが、実際のばらつきを “標準偏差” という値で直接的に表すのは難しいので、一般的に使われる指標と結び付けて考えたいところです。

そこで DARTSLIVE / PHOENIX のどちらのアプリでも自身の指標を確認できる、ソフトダーツの “ブル率” に着目し、このブル率と標準偏差との関係を求めていきたいと思います。

ブル率から $\sigma$ を求める

この計算をするにあたり、以下の条件を仮定します。

• ブルの中心を狙う $(\overline{x},\overline{y}) = (0,0)$
• 標準偏差 (ばらつき) が横方向および縦方向で同じとする $(\sigma = \sigma_x = \sigma_y)$

まず、ブルの中心を狙って半径 $R$ までに入る確率 $P(R) (0<P(R)<1)$ を考えます。これは $(x,y)$ について $(0,0)$ との距離が $R$ 以下になる確率を総合したもの、ということになります。積分を使って、式は以下のように書くことができます。

\[P(R) = \int_{0\leq x^2+y^2 \leq R^2}\frac{1}{2\pi\sigma^2}\exp\Bigl(-\frac{x^2+y^2}{2\sigma^2}\Bigr)dxdy\]

これを $x=r\cos\theta$、$y=r\sin\theta$ として、$r,\theta$ を用いる極座標系に変換すると、以下のように $P(R)$ は $R$ と $\sigma$ の関数で表すことができます。

\[\eqalign{ &= \int^{r=R}_{r=0}\int^{\theta=2\pi}_{\theta=0} \frac{1}{2\pi\sigma^2}\exp\Bigl(-\frac{r^2}{2\sigma^2}\Bigr)rd\theta dr \\ \\ &= \int^{r=R}_{r=0} \frac{r}{\sigma^2}\exp\Bigl(-\frac{r^2}{2\sigma^2}\Bigr) dr \\ \\ &= \Bigl[-\exp\Bigl(-\frac{r^2}{2\sigma^2}\Bigr)\Bigr]^R_0 \\ \\ P(R) &= 1 - \exp\Bigl(-\frac{R^2}{2\sigma^2}\Bigr) \;\;\; \cdots (2) \\ \\ }\]

これを$\sigma$についての式として変形すると、以下のようになります。

\[\sigma = \frac{R}{\sqrt{-2\log(1-P(R))}} \;\;\; \cdots (3)\]

ブル率は「ブルの中心を狙ってブル (半径22mm) に入る確率」です。つまりブル率を $P_B$ とすると $P_B=P(22)$ なので、$R=22{\rm (mm)}$ を式(3)に代入して以下のように表すことができます。

\[\sigma = \frac{22}{\sqrt{-2\log(1-P_B)}} \;\;\; \cdots (4)\]

これで、ブル率から $\sigma$ を求めることができるようになりました。いくつかのブル率で実際に標準偏差を求めてみた例を以下に示します。

ブル率(%)	標準偏差$\sigma$
10	47.9
30	26.0
50	18.7
70	14.2
90	10.3

$\sigma$と確率からグルーピング半径を求める

先ほどの式(3)を、$R$についての式として変形すると、

\[R = \sigma\sqrt{-2\log(1-P(R))} \;\;\; \cdots (5)\]

となります。式(3)でブル率から標準偏差を求めたうえで、任意の確率 $P(R)$ とともにこの式に代入してみると、対応するグルーピング半径 $R$ を求めることができます。ブル率を入れると、$R = 22({\rm mm})$ になりますし、たとえば 0.5 という値を入れると、「50%の確率でそこに到達する半径」を求めることができます。

標準偏差 $\sigma$ がもつ意味は？

式(5) の $\sqrt{-2\log(1-P(R))}$ が 1 のとき $R = \sigma$ となることから、その場合の $P(R)$ を導出してみます。

\[\eqalign{ \sqrt{-2\log(1-P(R))} &= 1 \\ -2\log(1-P(R)) &= 1 \\ \log(1-P(R)) &= -\frac{1}{2} \\ 1-P(R) &= e^{-\frac{1}{2}} \\ P(R) &= 1 - e^{-\frac{1}{2}} \\ &\approx 0.393 }\]

このことから、 $P(R) \approx 0.393$ の場合に $\sigma \approx R$ になるということがわかります。0.393 は 39.3% ということになりますので、おおよそ 5 本中 2 本程度到達させられるばらつきの半径が$\sigma$ということになります。先ほどの例でいうと、ブル率 90% では $\sigma = 10.3$ であり、ざっくり言うと 5 本中 2 本は狙った点から 10.3mm 以内の範囲に入れられるくらいのグルーピング、ということになります。

まとめ

本記事では、プログラミングでダーツを扱うために、

• 正規分布について
• 一般的な指標であるブル率から、正規分布を利用するために必要な指標である標準偏差 $\sigma$ を計算する
• 標準偏差 $\sigma$ の持つ意味

といったトピックを紹介しました。

ここまでの内容を応用して「インブル率を求める」「ある確率でグルーピングする範囲を求める」といったことができる Web アプリこちらに公開していますので、よろしければご覧ください(^ ^)/

ブル率とグルーピング | よしだラボ

最後までご覧いただき、ありがとうございました！

更新履歴

• 2023-02-17 数式の誤りを修正。 $\sigma$ の意味についての節を追加。
• 2022-02-05 初版

脚注・参考

1. A Statistician Plays Darts : イギリスの統計学者による論文。ハードダーツにおいてどこを狙うべきかをプレーヤーのレベルごとに統計学的なアプローチで求めている。正規分布を基本として、共分散の推定や歪正規分布を利用した、個々人に対して適用できるより高精度なモデルを提案している。 ↩ ↩²

2. ゼロワンでアガれる確率、全部シミュレーションしました。 : 犬のむせび鳴きblog : 正規分布を前提として、ゼロワンで上がる確率を乱数を用いたシミュレーションによって求めている記事(リンク切れ)。 ↩

3. 正規分布 - Wikipedia ↩

4. 多変量正規分布 - Wikipedia ↩

5. 直感を裏切る数学 「思い込み」にだまされない数学的思考法, 神永正博, p.91 「ダーツ実験における$x$の分布は、大数の法則を満たしません。ときどき出現する極端な値が、標本平均をドーンと変えてしまうわけです。」 ↩