前回の記事では、ダーツのスローが正規分布に従うと仮定することで、ブル率からインブル率を求めたり、グルーピング半径を求めたりする方法について紹介しました。

ゼロワンの最適なアレンジを算出しようとしたり、クリケットについて考えようと思うと、ブルまわりだけではダメで、各ナンバーのシングル・ダブル・トリプルを狙ってそこに到達する確率、というのも計算する必要があります。

そこで今回は数値積分を用いてダーツボード上の特定の位置を狙ったときに、任意のエリアに到達する確率を求める方法について考えてみたいと思います。

確率密度関数

正規分布に従うと仮定すると、ダーツを投げたときに任意の位置 (点$(x,y)$) に到達する確率は、狙った位置 (点$(\overline{x},\overline{y})$) と、縦横方向それぞれのばらつき $\sigma_x$ と $\sigma_y$ を用いて、 $f(x,y) = \frac{1}{2\pi\sigma_x\sigma_y}\exp\Bigl(-\Bigl(\frac{(x-\overline{x})^2}{2\sigma_x^2}+\frac{(y-\overline{y})^2}{2\sigma_y^2}\Bigr)\Bigr)$ と表すことができます。

この関数は確率密度関数といいます。これをプログラム上の関数として実装することを考えるのですが、ダーツボードの性質上、ここでは関数の入力を $(x,y,\overline{x},\overline{y})$ ではなく、半径と角度を用いる極座標系 $(r,\theta,\overline{r},\overline{\theta})$ とします。なお $\theta$ は、一般的なコンピュータグラフィックで右下を正とする座標系を用いることを考慮して、ブルから見て真右の “6” を $\theta=0$ として、時計回りに増えていく値を想定しています。

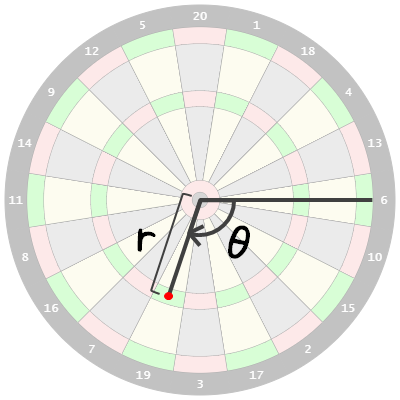
扱う座標系

以下は JavaScript で実際にコーディングしたものです。

// ---------------------------------------------------------------------------
//  prob_density : 確率密度関数
// ---------------------------------------------------------------------------
//  r : 確率導出対象の半径
//  t : 確率導出対象の偏角
// ar : 目標位置 (平均的に刺さる位置) に対応する半径
// at : 目標位置 (平均的に刺さる位置) に対応する偏角
// sx : x 方向の標準偏差
// sy : y 方向の標準偏差
static prob_density( r, t, ar, at, sx, sy ){
  var ax = ar * Math.cos(at);
  var ay = ar * Math.sin(at);
  var x  = r * Math.cos(t);
  var y  = r * Math.sin(t);
  var prob = 1.0 / ( 2 * Math.PI * sx * sy ) * Math.exp( - ( ( x - ax ) ** 2 / ( 2 * sx ** 2 ) + ( y - ay ) ** 2 / ( 2 * sy ** 2 ) ) );

  return prob;
}

この確率密度関数は $(r,\theta)$ という “点” に到達する確率を表しています。つまりこの関数だけでは T20 のような “面積のある領域” に到達する確率を求めることはできません。そこで、次はこの関数を使って「各エリアのいずれかに入る確率」を求める方法について考えていきたいと思います。

数値積分

あるエリアに入る場合、そのエリアの全ての領域で確率密度関数が同様の値をとるのであれば、単純に面積を掛けることによってエリア全体のどこかに到達する確率を求めることができるのですが、今回の場合は同じエリアであっても場所によって確率密度が異なるため、この関数を積分する必要があります。先ほど実装した確率密度関数に不定積分があれば比較的計算しやすいはずなのですが、残念ながら $f(x) = e^{-x^2}$ という形の関数には不定積分が存在しない¹ため、式を変形して直接的に積分値を求めることはできなさそうです。そこで、プログラミングでこれを求めるために数値積分という方法を利用することにします。

数値積分は以下の要領で行います。

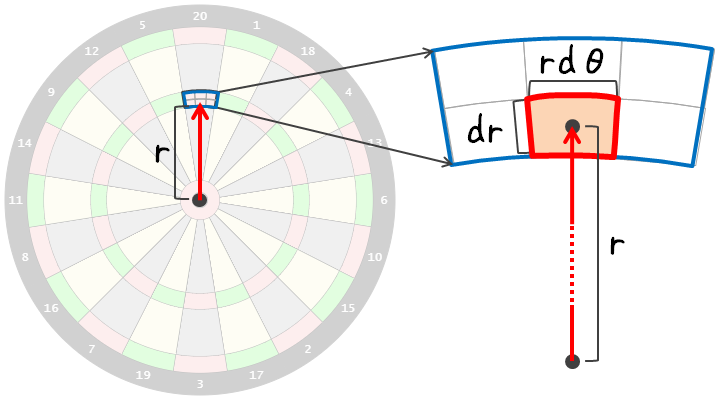
数値積分のイメージ

1. 対象の領域を $r$ 方向を $dr$ 単位で、$\theta$ 方向を $d\theta$ 単位で分割する
2. 分割領域を面積が $rd\theta \times dr$ の長方形²、領域内の確率密度は中心の値で一様と考えることで、この分割領域に到達する確率を近似的に求める
3. すべての分割領域に対して 2. を実施して和を求める

このようにして、エリア全体に到達する確率を近似的に求めることができます。上の図の例では $r$ 方向を 2 分割、$\theta$ 方向を 3 分割した例ですが、「領域内の確率密度は中心の値で一様と考える」という条件からわかるように、分割領域が小さいほど (分割数が多いほど) 近似の精度が上がります（同時に、それぞれの領域で確率密度を計算する必要があるので、演算に時間を要するようになります）。

こちらも JavaScript で実装した例を以下に示します。

// ---------------------------------------------------------------------------
//  prob_cumulative : 確率密度関数を指定範囲で数値積分した値を返す
// ---------------------------------------------------------------------------
// r0     : 数値積分対象の半径(min) (mm)
// r1     : 数値積分対象の半径(max) (mm)
// t0     : 数値積分対象の偏角(min) (radian)
// t1     : 数値積分対象の偏角(max) (radian)
// ar     : 目標位置 (平均的に刺さる位置) に対応する半径 (mm)
// at     : 目標位置 (平均的に刺さる位置) に対応する偏角 (radian)
// sx     : x 方向の標準偏差
// sy     : y 方向の標準偏差
// num_dr : 半径方向の分割数
// num_dt : 偏角方向の分割数
static prob_cumulative( r0, r1, t0, t1, ar, at, sx, sy, num_dr=20, num_dt=20 ){
  var total_prob = 0;

  var dr = Math.abs(r0-r1) * 1.0 / num_dr;
  var dt = Math.abs(t0-t1) * 1.0 / num_dt;

  for( var nr = 0 ; nr < num_dr ; nr++ ){
    var r  = Math.min(r0, r1) + ( dr * ( 2 * nr + 1 ) / 2 );
    var dS = r * dr * dt; // with Jacobian;
    for( var nt = 0 ; nt < num_dt ; nt++ ){
      var t = Math.min(t0, t1) + ( dt * ( 2 * nt + 1 ) / 2 );
      total_prob += this.prob_density( r, t, ar, at, sx, sy ) * dS;
    }
  }

  return total_prob;
}

分割数はデフォルト値で 20 としています。

前回の記事で、ブル率から $\sigma$ を求める方法を紹介しましたので、ブル率 30% の際の標準偏差 $\sigma = 26.0478…$ を用いて、ブルの中心を狙ってブルに入る確率 (＝ブル率) を逆に計算してみることにします。ブルの場合 $r$ は中心からブルの半径までになるので $(r_0, r_1) = ( 0, 22 )$、 $\theta$ は一周分になるので $(t_0, t_1) = (0, 2\pi)$ となります。また狙う位置は $(\overline{r},\overline{\theta})=(0,0)$ としています。

s = Math.sqrt(-(22*22)/(2*Math.log(1-0.3)))
26.04782000471105
prob_cumulative( 0, 22, 0, 2*Math.PI, 0, 0, s, s, 20, 20 )
0.30005941083278886
prob_cumulative( 0, 22, 0, 2*Math.PI, 0, 0, s, s, 50, 50 )
0.3000095038937735
prob_cumulative( 0, 22, 0, 2*Math.PI, 0, 0, s, s, 1000, 1000 )
0.30000002375885493

num_dr=20, num_dt=20 で $30.0059\%$、num_dr=50, num_dt=50 で $30.00009\%$ となり、分割数 20 でも 0.1% 以下の誤差で近似できていることがわかります。

この関数によって、$(\overline{r},\overline{\theta})$ を狙ってダーツを投げた際に、任意の領域 $(r_0\sim r_1,t_0\sim t_1)$ に到達する確率を求めることができるようになりました。

トリプルを狙った際に入る確率を求める

ここまでで実装した関数を使って、T20 を狙ったときに T20 に入る確率を求めてみます。

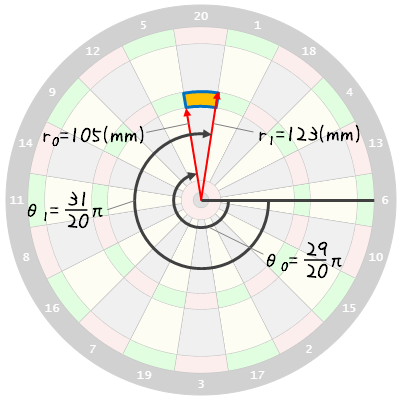
T20のパラメータ

ソフトダーツを想定し、上記のように T20 の範囲を $(r_0, r_1) = ( 105, 123 )$、 $\theta$ は $(t_0, t_1) = (\frac{29}{20}\pi, \frac{31}{20}\pi)$ とします。このちょうど真ん中にあたる $(\overline{r},\overline{\theta}) = ( 114, \frac{3}{2}\pi )$ を狙うとして「 T20 のど真ん中を狙って T20 に入る確率」をブル率別に求めてみましょう。

s = 22 * Math.sqrt(-1/(2*Math.log(1-0.1))) // ブル率 10%
prob_cumulative( 105, 123, Math.PI*29/20, Math.PI*31/20, 114, Math.PI*3/2, s, s, 1000, 1000 )
0.04339541056185865

s = 22 * Math.sqrt(-1/(2*Math.log(1-0.3))) // ブル率 30%
prob_cumulative( 105, 123, Math.PI*29/20, Math.PI*31/20, 114, Math.PI*3/2, s, s, 1000, 1000 )
0.13736045698490135

s = 22 * Math.sqrt(-1/(2*Math.log(1-0.5))) // ブル率 50%
prob_cumulative( 105, 123, Math.PI*29/20, Math.PI*31/20, 114, Math.PI*3/2, s, s, 1000, 1000 )
0.2449373045999073

s = 22 * Math.sqrt(-1/(2*Math.log(1-0.7))) // ブル率 70%
prob_cumulative( 105, 123, Math.PI*29/20, Math.PI*31/20, 114, Math.PI*3/2, s, s, 1000, 1000 )
0.3764083558506925

s = 22 * Math.sqrt(-1/(2*Math.log(1-0.9))) // ブル率 90%
prob_cumulative( 105, 123, Math.PI*29/20, Math.PI*31/20, 114, Math.PI*3/2, s, s, 1000, 1000 )
0.569944158450358

この結果をまとめると、以下のようになります！

ブル率(%)	T20を狙ってT20に入る確率(%)
10	4.34
30	13.74
50	24.49
70	37.64
90	56.99

ちなみに DARTSLIVE アプリで私の BULL 率と TRIPLE 率を確認したところ、それぞれ 37.0 %、18.2% でした。

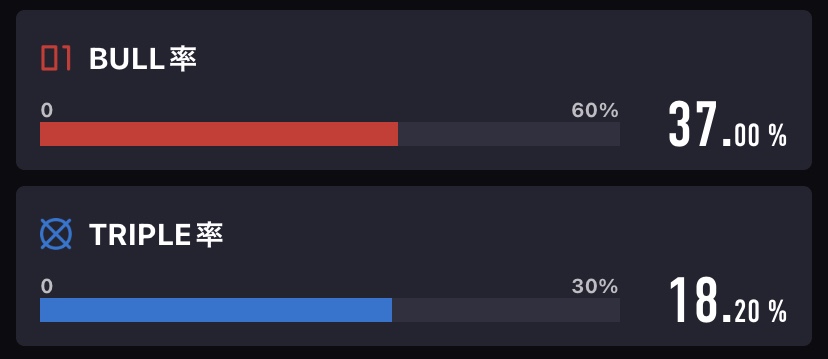
そこで、このブル率 37% から $\sigma$ を求めてこの関数に適用してみると、17.3% という結果になりました。シミュレーションとはいえ、大きく外してない感じがしますね！

まとめ

本記事では、ダーツのスローが正規分布に従う前提で、ある点を狙ってダーツを投げた場合に各エリアに入る確率を求める方法について検討しました。この仕組みを利用して、ねらい目を動かしたときにどのエリアにどれだけの確率で入るのかを可視化するツールがあります（前回紹介したものと同じものです）。

ブル率とグルーピング | よしだラボ

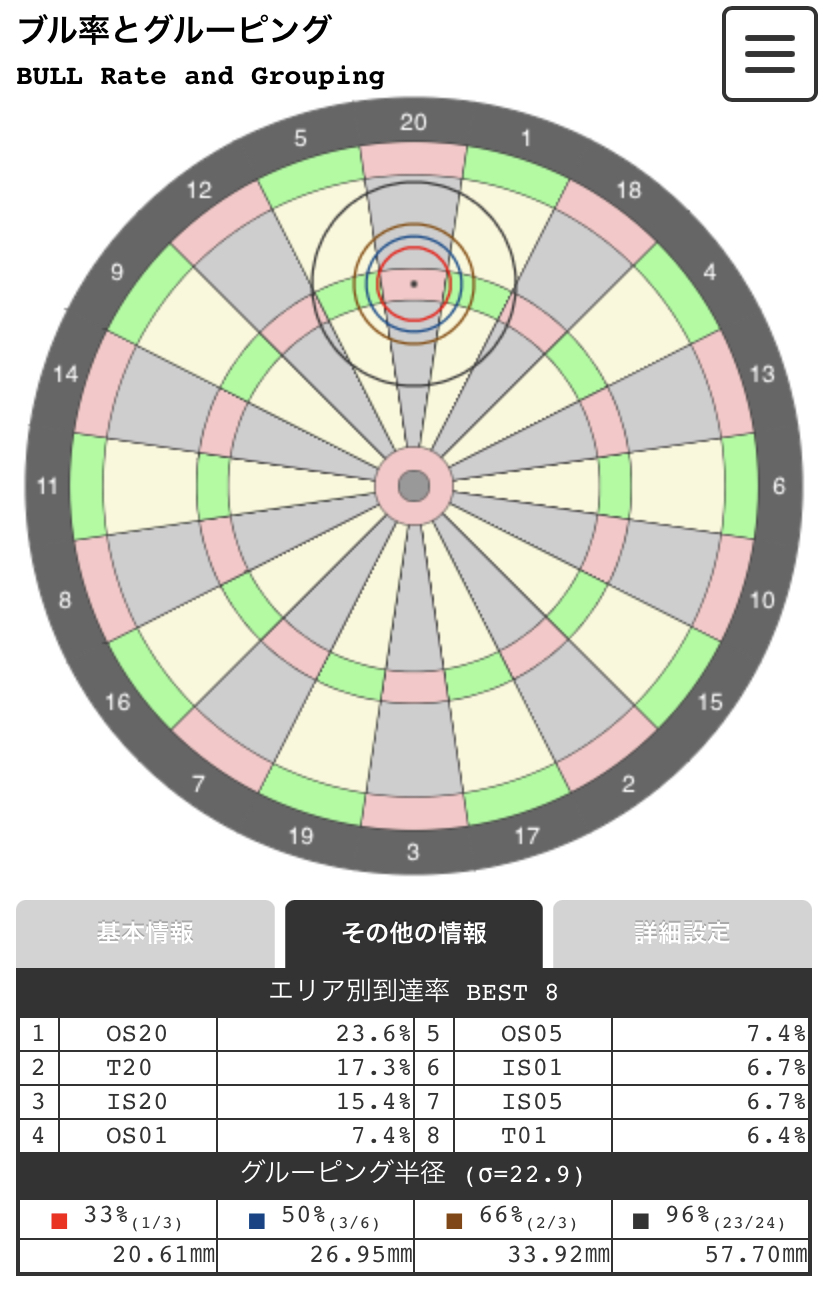
こんな感じで見ることができますので、よろしければ使ってみてください(^ ^)/

では、本日はこの辺で。最後までご覧いただき、ありがとうございました！

脚注・参考

1. ガウス積分 - Wikipedia 「初等関数としての不定積分 $\int e^{-x^2}dx$ は存在しないが、$\int^\infty_{-\infty} e^{-x^2}dx$ は評価することができるのである。」 ↩

2. ヤコビアン - EMANの物理数学 なぜ $\theta$ 方向が $rd\theta$ になるのかについてはこちらがわかりやすいです。 ↩