YouTubeチャンネル予備校のノリで学ぶ「大学の数学・物理」で最近公開された動画が興味深かったですよ！！

これはざっくり言うと「期待値がマイナスの『ゲームA』『ゲームB』に対して、この2つのゲームをコインの裏表で選択する『ゲームC』は期待値がプラスになる場合がある！」というもの。

詳細は動画を見ていただくとして、、今回は、実際に動画内で紹介されているゲームを Ruby でコーディングし、実際に 10 万回の試行を行うことで、本当にそんなことが起こるのかについて確認してみました。

# ----------------------------------------------------------------------------
# parrondo's-paradox.rb
# ----------------------------------------------------------------------------
# パロンドのパラドックスを乱数を使って確かめる
#  0~1 のランダムな値を返す rand() を使ってシミュレーションする
# ----------------------------------------------------------------------------

# ゲームA: 48% の確率で +1$、52% の確率で -1$
def gameA
  rand() <= 0.48 ? 1 : -1
end

# ゲームB: 所持金が 3 の倍数なら      1% の確率で +1$、99% の確率で -1$
#          所持金が 3 の倍数以外なら 85% の確率で +1$、15% の確率で -1$
def gameB( pos )
  ( ( pos % 3 ) == 0 ) ? ( rand() <= 0.01 ? 1 : -1 )
                       : ( rand() <= 0.85 ? 1 : -1 )
end

# ゲームC: 50%の確率でゲームA・ゲームBのどちらかを行う
def gameC( pos )
  rand() <= 0.5 ? gameA() : gameB(pos)
end

if $0 == __FILE__
  a, b, c = [0, 0, 0]
  trial_num = 100000
  trial_num.times{|i|
    a += gameA()
    b += gameB(b)
    c += gameC(c)
  }

  p [ a, b, c ]
end

実行してみます。全部で 7 回、合計 70 万回試行しましたが、いずれもゲームA・ゲームBの結果がマイナス、ゲームCの結果がプラスということがわかります！

$ ruby parrondos-paradox.rb
[-3466, -2446, 3036]
$ ruby parrondos-paradox.rb
[-4006, -2086, 3184]
$ ruby parrondos-paradox.rb
[-3906, -2238, 3148]
$ ruby parrondos-paradox.rb
[-3668, -2148, 3650]
$ ruby parrondos-paradox.rb
[-4172, -2094, 3166]
$ ruby parrondos-paradox.rb
[-3810, -2206, 3696]
$ ruby parrondos-paradox.rb
[-4348, -2212, 3482]

途中経過を残すようプログラムを修正し、グラフをプロットしてみました。

ゲームA/B/C それぞれの所持金比較

こちらでもゲームCの期待値だけがプラスになっていることが一目瞭然ですね。不思議ですねぇ～。面白いですね！

追試

せっかくなので、追試をしてみました。このゲーム全体でキモとなりそうなのが「ゲームBで所持金が3の倍数でない場合の勝率」のように感じたので、この確率を 1~99% で変化させてみた結果を求めてみました。

「ゲームBで所持金が3の倍数でない場合の勝率」を変えたときのゲームBの試行結果

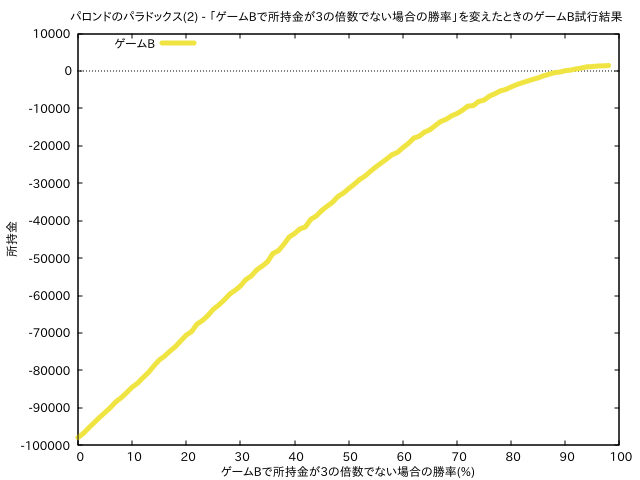
「ゲームBで所持金が3の倍数でない場合の勝率」を変えたときのゲームB試行結果

ゲームB単体の結果がこちらです。勝率が 90 %くらいでトントン、それ以下の場合は負けですね。感覚的に「所持金が3の倍数でない確率」は「所持金が3の倍数である確率」よりも2倍大きい気がするので 70% くらいあればで同じくらいになるのかと思っていましたが、実際は 90% くらいの勝率がないと同程度にならないというのが興味深いところ。

「ゲームBで所持金が3の倍数でない場合の勝率」を変えたときのゲームCの試行結果

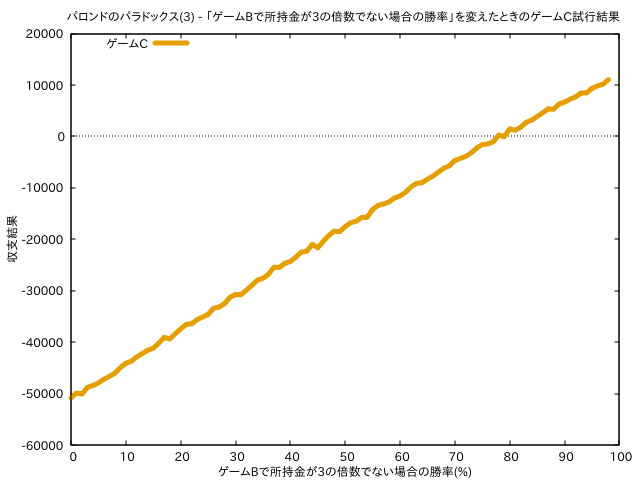
「ゲームBで所持金が3の倍数でない場合の勝率」を変えたときのゲームC試行結果

ゲームCの試行結果では単調増加のようなグラフとなりました。ゲームBで所持金が3の倍数でない場合の勝率が 80% くらいでトントンという感じですね。

ゲームCの結果はゲームBだけでなくゲームAの勝率も関係しますが、今回の条件の場合「ゲームBが単独で期待値マイナスになる」かつ「ゲームCで期待値がプラスになる」というちょうどいい値が 85% ということがわかりました。

まとめ

今回は Ruby によるプログラミングで、ヨビノリで紹介されていた「パロンドのパラドックス」について考察してみました！

本日使用したコードは こちら にありますので、興味のある方はご参照ください。

それでは、今日はこの辺で(^ ^)/